List of equations in fluid mechanics

This article summarizes equations in the theory of fluid mechanics.

DefinitionsEdit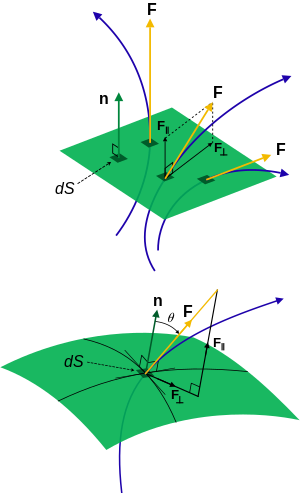

Flux F through a surface, dS is the differential vector area element, n is the unit normal to the surface. Left: No flux passes in the surface, the maximum amount flows normal to the surface. Right: The reduction in flux passing through a surface can be visualized by reduction in F or dS equivalently (resolved into components, θ is angle to normal n). F•dS is the component of flux passing through the surface, multiplied by the area of the surface (see dot product). For this reason flux represents physically a flow per unit area.

Here ${\displaystyle \mathbf {\hat {t}} \,\!}$ is a unit vector in the direction of the flow/current/flux.

Quantity (common name/s)	(Common) symbol/s	Defining equation	SI units	Dimension
Flow velocity vector field	u	${\displaystyle \mathbf {u} =\mathbf {u} \left(\mathbf {r} ,t\right)\,\!}$	m s−1	[L][T]−1
Velocity pseudovector field	ω	${\displaystyle {\boldsymbol {\omega }}=\nabla \times \mathbf {v} }$	s−1	[T]−1
Volume velocity, volume flux	φV (no standard symbol)	${\displaystyle \phi _{V}=\int _{S}\mathbf {u} \cdot \mathrm {d} \mathbf {A} \,\!}$	m3 s−1	[L]3 [T]−1
Mass current per unit volume	s (no standard symbol)	${\displaystyle s=\mathrm {d} \rho /\mathrm {d} t\,\!}$	kg m−3 s−1	[M] [L]−3 [T]−1
Mass current, mass flow rate	Im	${\displaystyle I_{\mathrm {m} }=\mathrm {d} m/\mathrm {d} t\,\!}$	kg s−1	[M][T]−1
Mass current density	jm	${\displaystyle I_{\mathrm {m} }=\iint \mathbf {j} _{\mathrm {m} }\cdot \mathrm {d} \mathbf {S} \,\!}$	kg m−2 s−1	[M][L]−2[T]−1
Momentum current	Ip	${\displaystyle I_{\mathrm {p} }=\mathrm {d} \left|\mathbf {p} \right|/\mathrm {d} t\,\!}$	kg m s−2	[M][L][T]−2
Momentum current density	jp	${\displaystyle I_{\mathrm {p} }=\iint \mathbf {j} _{\mathrm {p} }\cdot \mathrm {d} \mathbf {S} }$	kg m s−2	[M][L][T]−2

EquationsEdit

Physical situation	Nomenclature	Equations
Fluid statics, pressure gradient	r = Position ρ = ρ(r) = Fluid density at gravitational equipotential containing r g = g(r) = Gravitational field strength at point r ∇P = Pressure gradient	${\displaystyle \nabla P=\rho \mathbf {g} \,\!}$
Buoyancy equations	ρf = Mass density of the fluid Vimm = Immersed volume of body in fluid Fb = Buoyant force Fg = Gravitational force Wapp = Apparent weight of immersed body W = Actual weight of immersed body	Buoyant force ${\displaystyle \mathbf {F} _{\mathrm {b} }=-\rho _{f}V_{\mathrm {imm} }\mathbf {g} =-\mathbf {F} _{\mathrm {g} }\,\!}$ Apparent weight ${\displaystyle \mathbf {W} _{\mathrm {app} }=\mathbf {W} -\mathbf {F} _{\mathrm {b} }\,\!}$
Bernoulli's equation	pconstant is the total pressure at a point on a streamline	${\displaystyle p+\rho u^{2}/2+\rho gy=p_{\mathrm {constant} }\,\!}$
Euler equations	ρ = fluid mass density u is the flow velocity vector E = total volume energy density U = internal energy per unit mass of fluid p = pressure ${\displaystyle \otimes }$ denotes the tensor product	${\displaystyle {\frac {\partial \rho }{\partial t}}+\nabla \cdot (\rho \mathbf {u} )=0\,\!}$ ${\displaystyle {\frac {\partial \rho {\mathbf {u} }}{\partial t}}+\nabla \cdot \left(\mathbf {u} \otimes \left(\rho \mathbf {u} \right)\right)+\nabla p=0\,\!}$ ${\displaystyle {\frac {\partial E}{\partial t}}+\nabla \cdot \left(\mathbf {u} \left(E+p\right)\right)=0\,\!}$ ${\displaystyle E=\rho \left(U+{\frac {1}{2}}\mathbf {u} ^{2}\right)\,\!}$
Convective acceleration		${\displaystyle \mathbf {a} =\left(\mathbf {u} \cdot \nabla \right)\mathbf {u} }$
Navier–Stokes equations	TD = Deviatoric stress tensor ${\displaystyle \mathbf {f} }$ = volume density of the body forces acting on the fluid ${\displaystyle \nabla }$ here is the del operator.	${\displaystyle \rho \left({\frac {\partial \mathbf {u} }{\partial t}}+\mathbf {u} \cdot \nabla \mathbf {u} \right)=-\nabla p+\nabla \cdot \mathbf {T} _{\mathrm {D} }+\mathbf {f} }$

This article uses material from the Wikipedia article  Metasyntactic variable, which is released under the  Creative Commons Attribution-ShareAlike 3.0 Unported License.