Nonlinear frictiophoresis

Nonlinear frictiophoresis is the unidirectional drift of a particle in a medium caused by periodic driving force with zero mean. The effect is possible due to nonlinear dependence of the friction-drag force on the particle's velocity. It was discovered theoretically.,^[1] and is mainly known as nonlinear electrofrictiophoresis ^[1] .^[2] At first glance, a periodic driving force with zero mean is able to entrain a particle into an oscillating movement without unidirectional drift, because integral momentum provided to the particle by the force is zero. The possibility of unidirectional drift can be recognized if one takes into account that the particle itself loses momentum through transferring it further to the medium it moves in/at. If the friction is nonlinear, then it may so happen that the momentum loss during movement in one direction does not equal to that in the opposite direction and this causes unidirectional drift. For this to happen, the driving force time-dependence must be more complicated than it is in a single sinusoidal harmonic.

A simple example - Bingham plasticEdit

Nonlinear frictionEdit

The simplest case of friction-velocity dependence law is the Stokes's one:

${\displaystyle (1)\qquad F_{dr}(v)=\lambda v,}$

where ${\displaystyle F_{dr}(v)}$ is the friction/drag force applied to a particle moving with velocity ${\displaystyle v}$ in a medium. The friction-velocity law (1) is observed for a slowly moving spherical particle in a Newtonian fluid.

Fig. 1 Linear friction

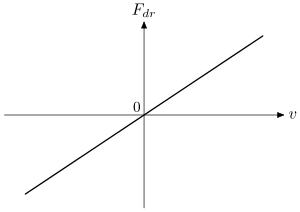
It is linear, see Fig. 1, and is not suitable for nonlinear frictiophoresis to take place. The characteristic property of the law (1) is that any, even a very small driving force is able to get particle moving. This is not the case for such media as Bingham plastic. For those media, it is necessary to apply some threshold force, ${\displaystyle d}$, to get the particle moving. This kind of friction-velocity (dry friction) law has a jump discontinuity at ${\displaystyle v=0}$:

${\displaystyle (2)\qquad F_{dr}(v)=\lambda v+d\cdot \mathrm {sign} (v).}$

Fig. 2 Nonlinear friction example

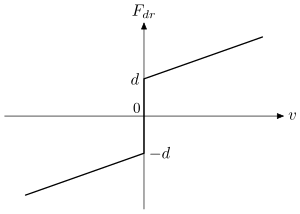
It is nonlinear, see Fig. 2, and is used in this example.

Periodic driving forceEdit

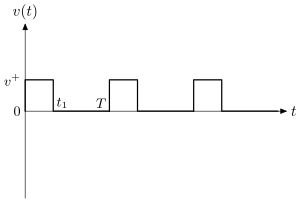
Let ${\displaystyle T>0}$ denote the period of driving force. Chose a time value ${\displaystyle t_{1}}$ such that ${\displaystyle 0<t_{1}<T}$ and two force values, ${\displaystyle F^{+}>0}$, ${\displaystyle F^{-}<0}$ such that the following relations are satisfied:

${\displaystyle \qquad \qquad F^{+}>d,\quad |F^{-}|<d,}$

${\displaystyle (3)\qquad F^{+}t_{1}+F^{-}(T-t_{1})=0.}$

The periodic driving force ${\displaystyle f(t)}$ used in this example is as follows:

${\displaystyle (4)\qquad f(t)={\begin{cases}F^{+},{\text{ if }}0<t\leq t_{1},\\F^{-},{\text{ if }}t_{1}<t\leq T,\quad f(t+T)=f(t).\end{cases}}}$

It is clear that, due to (3), ${\displaystyle f(t)}$ has zero mean:

${\displaystyle \int \limits _{0}^{T}f(t)dt=F^{+}t_{1}+F^{-}(T-t_{1})=0.}$

Fig. 3 Zero mean driving force example

See also Fig. 3.

Unidirectional driftEdit

For the sake of simplicity, we consider here the physical situation when inertia may be neglected. The latter can be achieved if particle's mass is small, velocity is low and friction is high. This conditions have to ensure that ${\displaystyle \tau \ll t_{1}}$, where ${\displaystyle \tau }$ is the relaxation time. In this situation, the particle driven with force (4) immediately starts moving with constant velocity ${\displaystyle v^{+}={\frac {1}{\lambda }}(F^{+}-d)}$ during interval ${\displaystyle 0<t\leq t_{1}}$ and will immediately stop moving during interval ${\displaystyle t_{1}<t\leq T}$, see Fig. 4.

Fig. 4 Velocity with nonzero mean

This results in the positive mean velocity of unidirectional drift:

${\displaystyle \qquad \qquad {\overline {v(t)}}={\frac {1}{T}}\int \limits _{0}^{T}v(t)dt={\frac {t_{1}}{\lambda T}}(F^{+}-d)>0.}$

Mathematical analysisEdit

Analysis of possibility to get a nonzero drift by periodic force with zero integral has been made in .^[1] The dimensionless equation of motion for a particle driven by periodic force ${\displaystyle f(t)}$, ${\displaystyle f(t+1)=f(t)}$, ${\displaystyle \int _{0}^{1}f(t)dt=0}$ is as follows:

${\displaystyle (5)\qquad {\dot {v}}+\lambda v-\epsilon g(v)=f(t),}$

where the friction/drag force ${\displaystyle F_{dr}(v)=\lambda v-\epsilon g(v)}$ satisfies the following:

${\displaystyle \qquad \qquad F_{dr}(-v)=-F_{dr}(v),\quad {\frac {d}{dv}}F_{dr}(v)\geq 0.}$

It is proven in ^[1] that any solution to (5) settles down onto periodic regime ${\displaystyle v^{*}(t)}$, ${\displaystyle v^{*}(t+1)=v^{*}(t)}$, which has nonzero mean:

${\displaystyle \qquad \qquad {\overline {v^{*}(t)}}=\int \limits _{0}^{1}v^{*}(t)dt\neq 0,}$

almost certainly, provided ${\displaystyle f(t)}$ is not antiperiodic.^[3]

For ${\displaystyle g(v)=v^{3}}$, two cases of ${\displaystyle f(t)}$ have been considered explicitly:

1. Saw-shaped driving force, see Fig. 5:

Fig. 5 Saw-shaped driving force

${\displaystyle \qquad \qquad f(t)=at,\quad t\in [-1/2;1/2],\quad f(t+1)=f(t),\quad t\in ]-\infty ;\infty [.}$

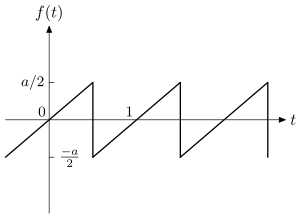
In this case, found in ^[1] first order in ${\displaystyle \epsilon }$ approximation to ${\displaystyle v^{*}(t)}$, ${\displaystyle v_{1}^{*}(t)}$, has the following mean value:

${\displaystyle \qquad \qquad {\Big |}{\overline {v_{1}^{*}(t)}}{\Big |}\equiv {\Big |}\int \limits _{0}^{1}v_{1}^{*}(t)dt{\Big |}\geq {\frac {2}{3}}\epsilon a^{3}/\lambda ^{5}.}$

This estimate is made expecting ${\displaystyle \lambda \gg 1}$.

2. Two harmonics driving force,

${\displaystyle \qquad \qquad f(t)=a\cos(2\pi t)+b\cos(4\pi t+\psi ).}$

In this case, the first order in ${\displaystyle \epsilon }$ approximation has the following mean value:

${\displaystyle \qquad \qquad {\Big |}{\overline {v_{1}^{*}(t)}}{\Big |}={\Big |}\int \limits _{0}^{1}v_{1}^{*}(t)dt{\Big |}\geq {\frac {2}{27}}{\frac {\epsilon }{\lambda }}\left({\frac {M}{\lambda }}\right)^{3}{\frac {1}{(1+{\frac {4\pi ^{2}}{\lambda ^{2}}})(1+{\frac {16\pi ^{2}}{\lambda ^{2}}})^{1/2}}}.}$

This value is maximized in ${\displaystyle \psi }$, ${\displaystyle a,b}$, keeping ${\displaystyle a+b=M}$ constant. Interesting that the drift value depends on ${\displaystyle \psi }$ and changes its direction twice as ${\displaystyle \psi }$ spans over the interval ${\displaystyle [0;2\pi ]}$. Another type of analysis,^[4] based on symmetry breaking suggests as well that a zero mean driving force is able to generate a directed drift.

ApplicationsEdit

Fig.6 (a): solid line -- the drag force per charge on single b.p. vs velocity, dotted line -- linear approximation for comparison. (b): same as (a), but in fine scale

In applications, the nature of force ${\displaystyle f(t)}$ in (5), is usually electric, similar to forces acting during standard electrophoresis. The only differences are that the force is periodic and without constant component.

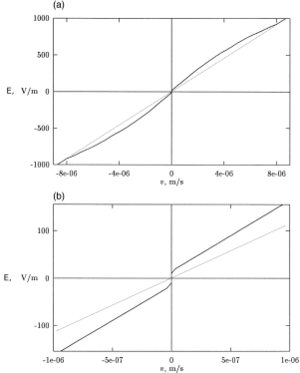
For the effect to show up, the dependence of friction/drag force on velocity must be nonlinear. This is the case for numerous substances known as non-Newtonian fluids. Among these are gels, and dilatant fluids, pseudoplastic fluids, liquid crystals. ^[5] Dedicated experiments^[2] have determined ${\displaystyle F_{dr}(v)}$ for a standard DNA ladder up to 1500 bp long in 1.5% agarose gel. The dependence found, see Fig. 6, supports the possibility of nonlinear frictiophoresis in such a system. Based on data in Fig. 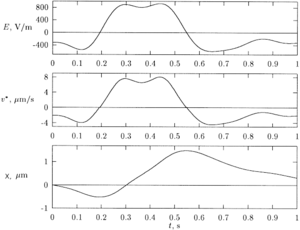6, an optimal time course for driving electric field with zero mean, ${\displaystyle E(t)}$, has been found in,^[2] which ensures maximal drift for 1500 b.p. long fragment, see Fig. 7.

Fig. 7 Time courses of optimal electric field, ${\displaystyle E(t)}$, ${\displaystyle E(t\pm 1s)=E(t)}$, steady-state velocity, ${\displaystyle v^{*}(t)}$, and displacement, ${\displaystyle X(t)}$. The drift value ${\displaystyle {\overline {v^{*}(t)}}=0.31\mu }$m/s.

The effect of unidirectional drift caused by periodic force with zero integral value has a peculiar dependence on the time course of the force applied. See the previous section for examples. This offers a new dimension to a set of separation problems.

DNA separation with respect to lengthEdit

In the DNA fragments separation, zero mean periodic electric field is used in zero-integrated-field electrophoresis (ZIFE),^[6] where the field time dependence similar to that shown in Fig. 3 is used. This allows to separate long fragments in agarose gel, nonseparable by standard constant field electrophoresis. The long DNA geometry and its manner of movement in a gel, known as reptation do not allow to apply directly the consideration based on Eq. (5), above.

Separation with respect to specific massEdit

It was observed, ^[7] that under certain physical conditions the mechanism described in Mathematical analysis section, above, can be used for separation with respect to specific mass, like particles made of isotopes of the same material.

ExtensionsEdit

The idea of organizing directed drift with zero mean periodic drive have obtained further development for other configurations and other physical mechanism of nonlinearity.

Rotation by means of circular waveEdit

An electric dipole rotating freely around ${\displaystyle z}$-axis in a medium with nonlinear friction can be manipulated by applying electromagnetic wave polarized circularly along ${\displaystyle \pm z}$ and composed of two harmonics. The equation of motion for this system is as follows:

${\displaystyle \qquad \qquad {\dot {\omega }}+\lambda \omega -\epsilon g(\omega )=f(t,\theta (t)),\quad {\dot {\theta }}=\omega ,}$

where ${\displaystyle f(t,\theta (t))}$ is the torque acting on the dipole due to circular wave:

${\displaystyle (6)\qquad f(t,\theta (t))\sim |p|(A_{1}\cos(\omega t\pm \theta )+A_{2}\cos(2\omega t\pm \theta +\psi )),}$

where ${\displaystyle p}$ is the dipole moment component orthogonal to ${\displaystyle z}$-axis and ${\displaystyle \theta }$ defines the dipole direction in the ${\displaystyle XY}$ plane. By choosing proper phase shift ${\displaystyle \psi }$ in (6) it is possible to orient the dipole in any desired direction, ${\displaystyle \theta _{0}}$. The direction ${\displaystyle \theta _{0}}$ is attained due to angular directed drift, which becomes zero when ${\displaystyle \theta =\theta _{0}}$. ^[8][9] A small detuning between the first and second harmonic in (6) results in continuous rotational drift.^[9]

Modification of potential functionEdit

Fig. 8 Example of modification of potential function ${\displaystyle U(x)}$ due to nonlinear frictiophoresis. (a) initial ${\displaystyle U(x)}$, (b) modified ${\displaystyle U(x)}$.

If a particle undergoes a directed drift while moving freely in accordance with Eq. (5), then it drifts similarly if a shallow enough potential field ${\displaystyle U(x)}$ is imposed. Equation of motion in that case is:

${\displaystyle \qquad \qquad {\dot {v}}+\lambda v-\epsilon g(v)=f(t)-\phi (x),\quad {\dot {x}}=v,}$

where ${\displaystyle \phi (x)}$ is the force due to potential field. The drift continues until a steep enough region in the course of ${\displaystyle U(x)}$ is met, which is able to stop the drift. This kind of behavior, as rigorous mathematical analysis shows, ^[10] results in modification of ${\displaystyle U(x)}$ by adding a linear in ${\displaystyle x}$ term. This may change the ${\displaystyle U(x)}$ qualitatively, by, e.g. changing the number of equilibrium points, see Fig. 8. The effect may be essential during high frequency electric field acting on biopolymers. ^[11]

Another nonlinearityEdit

For electrophoresis of colloid particles under a small strength electric field, the force ${\displaystyle f(t)}$ in the right-hand side of Eq. (5) is linearly proportional to the strength ${\displaystyle E(t)}$ of the electric field applied. For a high strength, the linearity is broken due to nonlinear polarization. As a result, the force may depend nonlinearly on the applied field:

${\displaystyle \qquad \qquad f(t)\sim E(t)+\alpha (E(t))^{3}.}$

In the last expression, even if the applied field,  has zero mean, the applied force  may happen to have a constant component that can cause a directed drift. ^[12] As above, for this to happen,  must have more than a single sinusoidal harmonic. This same effect for a liquid in a tube may serve in electroosmotic pump driven with zero mean electric field. 

This article uses material from the Wikipedia article  Metasyntactic variable, which is released under the  Creative Commons Attribution-ShareAlike 3.0 Unported License.